en alternativ normalitetstest er Shapiro-vilk-testen.

• hvad er en Kolmogorov-Smirnov normalitetstest?
• SPSS Kolmogorov-Smirnov test fra NPAR Test
• SPSS Kolmogorov-Smirnov test fra Undersøg variabler
• rapportering af en Kolmogorov-Smirnov Test
• forkerte resultater i SPSS?

hvad er en Kolmogorov-Smirnov normalitetstest?

Kolmogorov-Smirnov-testen undersøger, om scoringer
sandsynligvis vil følge en vis fordeling i en eller anden befolkning.For at undgå forvirring er der 2 Kolmogorov-Smirnov tests:

• Der er den ene prøve Kolmogorov-Smirnov test til test, hvis en variabel følger en given fordeling i en population. Denne ” givne fordeling “er normalt-ikke altid – den normale fordeling, derfor”Kolmogorov-Smirnov normalitetstest”.
• Der er også den (meget mindre almindelige) uafhængige prøver Kolmogorov-Smirnov test til test, hvis en variabel har identiske fordelinger i 2 populationer.

i teorien kunne “Kolmogorov-Smirnov-test” henvise til begge test (men henviser normalt til Kolmogorov-Smirnov-testen med en prøve) og havde bedre undgås. Forresten er begge Kolmogorov-Smirnov-tests til stede i SPSS.

Kolmogorov-Smirnov Test – simpelt eksempel

så siger jeg har en befolkning på 1.000.000 mennesker. Jeg tror, at deres reaktionstider på en eller anden opgave er perfekt normalt fordelt. Jeg prøver 233 af disse mennesker og måler deres reaktionstider.
nu vil den observerede frekvensfordeling af disse sandsynligvis afvige lidt-men ikke for meget – fra en normalfordeling. Så jeg kører et histogram over observerede reaktionstider og overlejrer en normalfordeling med samme middel-og standardafvigelse. Resultatet er vist nedenfor.

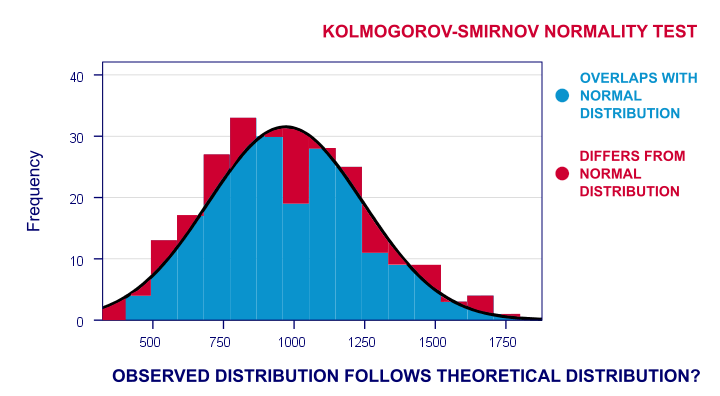
frekvensfordelingen af mine scoringer overlapper ikke helt med min normale kurve. Nu kunne jeg beregne procentdelen af sager, der afviger fra den normale kurve-procentdelen af røde områder i diagrammet. Denne procentdel er en teststatistik: den udtrykker i et enkelt tal, hvor meget mine data adskiller sig fra min nulhypotese. Så det angiver, i hvilket omfang de observerede scoringer afviger fra en normal fordeling.
nu, hvis min nulhypotese er sand, så skal denne afvigelsesprocent nok være ret lille. Det vil sige, en lille afvigelse har en høj sandsynlighedsværdi eller p-værdi.
omvendt er en enorm afvigelsesprocent meget usandsynlig og antyder, at mine reaktionstider ikke følger en normal fordeling i hele befolkningen. Så en stor afvigelse har en lav p-værdi. Som tommelfingerregel blev nulhypotesen udsat, hvis p < 0.05.So hvis p < 0.05, tror vi ikke, at vores variabel følger en normal fordeling i vores befolkning.

Kolmogorov-Smirnov Test – teststatistik

så det er den nemmeste måde at forstå, hvordan Kolmogorov-Smirnov-normalitetstesten fungerer. Beregningsmæssigt fungerer det imidlertid forskelligt: det sammenligner det observerede versus de forventede kumulative relative frekvenser som vist nedenfor.

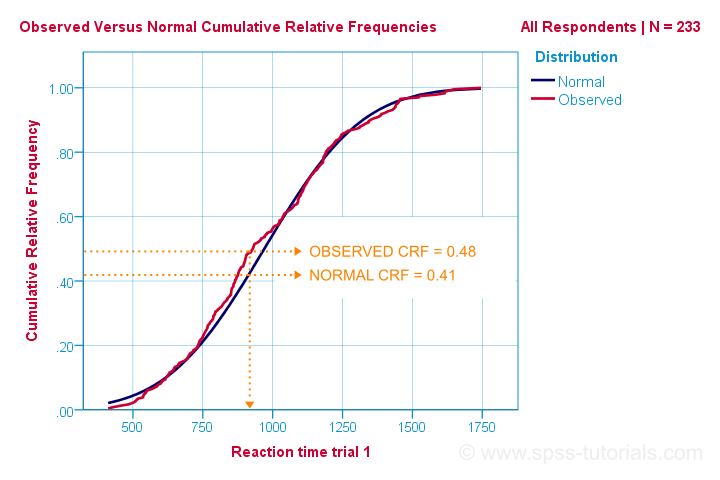
Kolmogorov – Smirnov-testen bruger den maksimale absolutte forskel mellem disse kurver som dens teststatistik betegnet med D. i dette diagram er den maksimale absolutte forskel D (0,48 – 0,41 =) 0,07, og den forekommer ved en reaktionstid på 960 millisekunder. Husk, at D = 0,07, da vi støder på det i vores SPSS-output om et minut.

Kolmogorov-Smirnov-testen i SPSS

der er 2 måder at køre testen i SPSS:

• NPAR TESTS som fundet under analyse Nonparametric Tests 1-Prøve K-S… er vores metode til valg, fordi det skaber pænt detaljeret output.
• Undersøg variabler fra analyser Beskrivende statistik Udforsk er et alternativ. Denne kommando kører både Kolmogorov-Smirnov-testen og Shapiro-vilk-normalitetstesten.
  bemærk, at Undersøg variabler bruger listevis udelukkelse af manglende værdier som standard. Så hvis jeg tester 5 variabler, bruger mine 5 tests kun sager, der ikke har nogen missings på nogen af disse 5 variabler. Dette er normalt ikke, hvad du vil, men vi viser, hvordan du undgår dette.

vi demonstrerer begge metoder ved hjælp af speedtasks.sav hele, hvoraf en del er vist nedenfor.

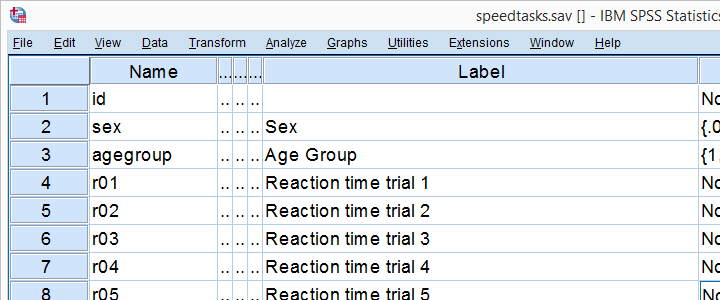
vores vigtigste forskningsspørgsmål erhvilken af reaktionstidsvariablerne er sandsynligvis
at blive normalt fordelt i vores befolkning?Disse data er et lærebogseksempel på, hvorfor du skal inspicere dine data grundigt, før du begynder at redigere eller analysere dem. Lad os gøre netop det og køre nogle histogrammer fra syntaksen nedenfor.

resultat

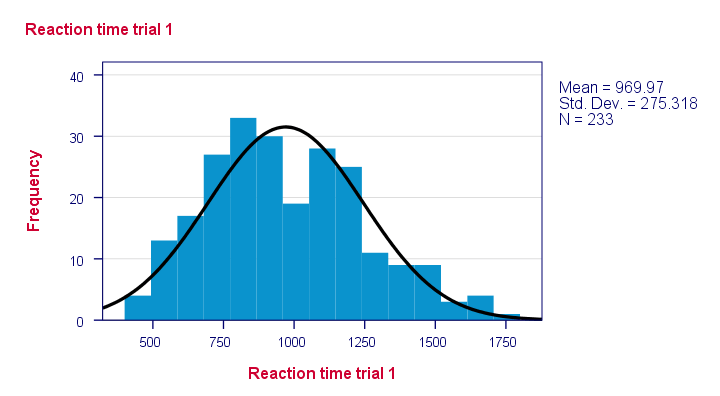
Bemærk, at nogle distributioner slet ikke ser plausible ud. Men hvilke vil sandsynligvis blive distribueret normalt?

SPSS Kolmogorov-Smirnov test fra NPAR test

vores foretrukne mulighed for at køre Kolmogorov-Smirnov test er underanalyse Legacy dialoger 1-prøve K-S… som vist nedenfor.

næste, vi bare udfylde dialogen som vist nedenfor.

Klik på Indsæt resultater i syntaksen nedenfor. Lad os køre det.

Kolmogorov-Smirnov Test syntaks fra Nonparametric Tests

resultater

først skal du bemærke, at teststatistikken for vores første variabel er 0.073-ligesom vi så i vores kumulative relative frekvensdiagram lidt tidligere. Diagrammet indeholder nøjagtigt de samme data, som vi lige har kørt vores test på, så disse resultater konvergerer pænt.
vedrørende vores forskningsspørgsmål: kun reaktionstiderne for forsøg 4 synes at være normalt fordelt.

SPSS Kolmogorov-Smirnov test fra Undersøg variabler

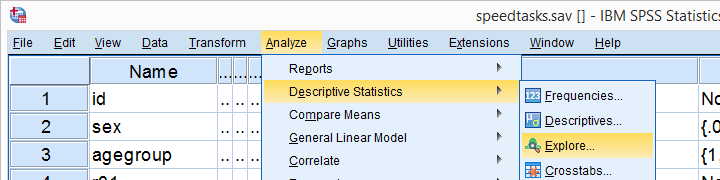
en alternativ måde at køre Kolmogorov-Smirnov test starter fra analysere Beskrivende statistik Udnyttelsesområder vist nedenfor.

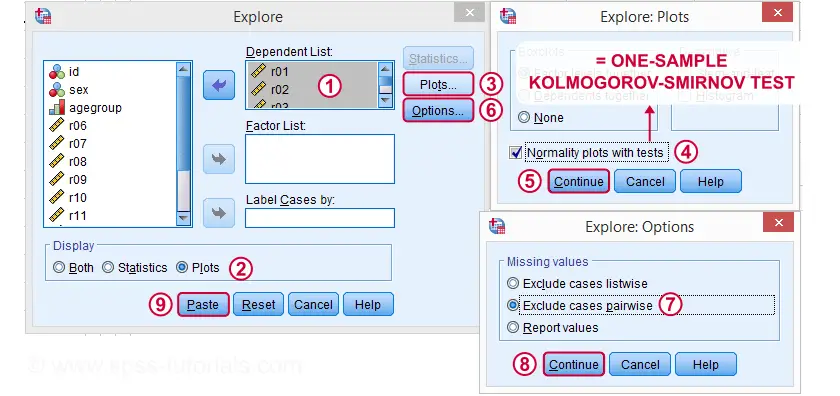
Kolmogorov-Smirnov Test syntaks fra ikke-parametriske Tests

Results

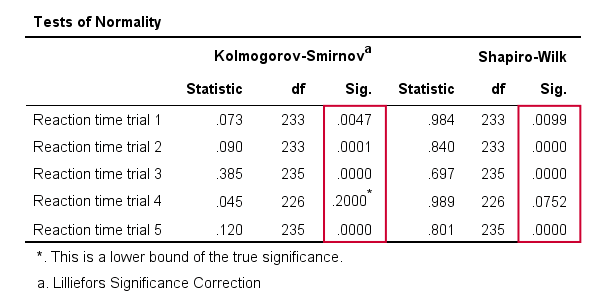
As a rule of thumb, we conclude thata variable is not normally distributed if “Sig.” < 0.05.Så både Kolmogorov-Smirnov-testen såvel som Shapiro-vilk-testresultaterne antyder, at kun Reaktionstidsforsøg 4 følger en normal fordeling i hele befolkningen.
Bemærk endvidere, at Kolmogorov-Smirnov-testresultaterne er identiske med dem, der opnås fra NPAR-test.

rapportering af en Kolmogorov-Smirnov-Test

for at rapportere vores testresultater efter APA-retningslinjer skriver vi noget som”en Kolmogorov-Smirnov-test indikerer, at reaktionstiderne i forsøg 1 ikke følger en normal fordeling, D(233) = 0,07, p = 0,005.”For yderligere variabler, prøv at forkorte dette, men sørg for at inkludere

• D (for “forskel”), Kolmogorov-Smirnov teststatistik,
• df, frihedsgraderne (som er lig med N) og
• p, den statistiske signifikans.

forkerte resultater i SPSS?

Hvis du er studerende, der bare vil bestå en prøve, kan du stoppe med at læse nu. Bare Følg de trin, vi diskuterede indtil videre, så bliver du god.

højre, lad os nu køre de nøjagtige samme tests igen i SPSS version 18 og se på output.

i denne output er de nøjagtige p-værdier inkluderet og-heldigvis – de er meget tæt på de asymptotiske p-værdier. Mindre heldigvis er SPSS version 18 resultaterne vildt forskellige
fra SPSS version 24 resultatervi rapporterede hidtil.
årsagen synes at være Lilliefors betydning korrektion, som anvendes i nyere SPSS versioner. Resultatet ser ud til at være, at de asymptotiske signifikansniveauer adskiller sig meget mere fra den nøjagtige betydning, end de gjorde, når korrektionen ikke er underforstået. Dette rejser alvorlig tvivl om rigtigheden af” Lilliefors-resultaterne ” – standard i nyere SPSS-versioner.
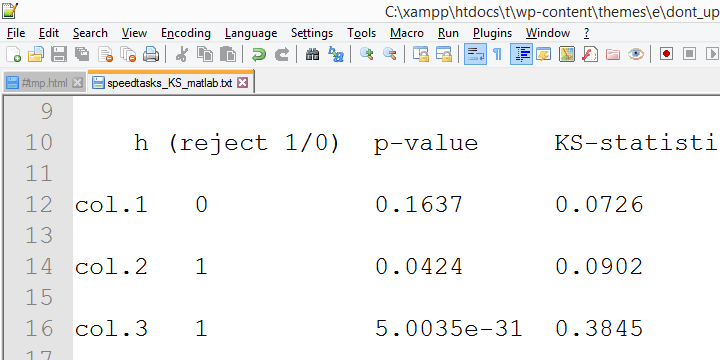
konvergerende beviser for dette forslag blev samlet af min kollega Alvin Stegeman, der omlægger alle tests i Matlab. Matlab-resultaterne stemmer overens med SPSS 18-resultaterne og – dermed-ikke med de nyere resultater.

Kolmogorov-Smirnov normalitetstest – begrænset anvendelighed

Kolmogorov-Smirnov-testen er ofte at teste den normalitetsantagelse, der kræves af mange statistiske tests som ANOVA, t-testen og mange andre. Det er imidlertid næsten rutinemæssigt overset, at sådanne tests er robuste mod en overtrædelse af denne antagelse, hvis stikprøvestørrelser er rimelige, siger n LR 25.Den underliggende årsag til dette er den centrale grænse sætning. Derfor er normalitetstest kun nødvendig for små prøvestørrelserhvis målet er at tilfredsstille normalitetsantagelsen.
desværre resulterer små stikprøvestørrelser i lav statistisk effekt til normalitetstest. Dette betyder, at væsentlige afvigelser fra normalitet ikke vil resultere i statistisk signifikans. Testen siger, at der ikke er nogen afvigelse fra normalitet, mens den faktisk er enorm. Kort sagt er situationen, hvor normalitetstest er nødvendig-små stikprøvestørrelser – også den situation, hvor de klarer sig dårligt.

tak for læsning.