Articles

abstrakte datastrukturer

by admin

abstrakte datatyper

i datalogi er en abstrakt datatype (ADT) en matematisk model for datatyper, hvor en datatype er defineret af dens adfærd (semantik) set fra en bruger af dataene, specifikt med hensyn til mulige værdier, mulige operationer på data af denne type og opførslen af disse operationer. Dette står i kontrast til datastrukturer, som er konkrete repræsentationer af data, og er synspunktet for en implementer, ikke en bruger.

formelt kan en ADT defineres som en “klasse af objekter, hvis logiske opførsel er defineret af et sæt værdier og et sæt operationer”; dette er analogt med en algebraisk struktur i matematik. Hvad der menes med “adfærd” varierer efter forfatter, hvor de to hovedtyper af formelle specifikationer for adfærd er aksiomatisk (algebraisk) specifikation og en abstrakt model; disse svarer til henholdsvis aksiomatisk semantik og operationel semantik i en abstrakt maskine. Nogle forfattere inkluderer også beregningskompleksiteten (“omkostninger”), både med hensyn til tid (til computeroperationer) og plads (til repræsentation af værdier).

grunden til, at vi bruger abstrakte strukturer, er fordi de effektivt bruger hukommelse baseret på designet af de data, der er gemt i dem. Med meget store mængder data eller meget ofte skiftende data kan datastrukturen gøre en enorm forskel i effektiviteten (køretid) af dit computerprogram.

på mere almindeligt sprog er en abstrakt datastruktur blot et arrangement af data, som vi har indbygget i et ordnet arrangement.

en perfekt dejlig oversigt

nogle typer abstrakte datastrukturer

vurderet af IB

  1. statisk og dynamisk datastruktur
  1. arrays
  2. todimensionale arrays
  3. stak
  4. kø
  5. linked list
  6. træ
  7. binær træ
  8. samlinger
  9. rekursion

ikke vurderet af Ib, men du bør kende dem

  1. lister
  2. ordbøger
  3. sæt
  4. tuple

grundlæggende operationer af datastrukturer

jeg fandt dette fremragende dias fra Simon allardice.

grundlæggende operationer af arrays.png

sammenligning af forskellige datastrukturer

datastruktur styrker svagheder
arrays indsættelse og sletning af elementer, iterering gennem samlingen sortering og søgning, indsættelse og sletning – især hvis du indsætter og sletter i begyndelsen eller slutningen af arrayet
linked list direkte indeksering, let at oprette og bruge direkte adgang, søgning og sortering
stak og kø designet til LIFO / FIFO direkte adgang, søgning og sortering
binært træ hastighed for indsættelse og sletning, adgangshastighed, vedligeholdelse af sorteret rækkefølge nogle overhead

  • faste strukturer er hurtigere / mindre
  • når du overvejer, om du skal bruge en abstrakt datastruktur, skal du spørge dig selv: hvad indeholder flest data, og hvad indeholder de hyppigst ændrede data?

sammenligning af statiske vs dynamiske datastrukturer

denne sammenligning bruges fra vores Computer science lærebog.

statisk datastruktur dynamisk datastruktur
ineffektiv, da hukommelse er allokeret, som muligvis ikke er nødvendig. effektiv, da mængden af hukommelse varierer efter behov.
hurtig adgang til hvert element af data, da hukommelsesplaceringen er fast, når programmet er skrevet. langsommere adgang til hvert element, da hukommelsesplaceringen tildeles ved kørselstid.
hukommelsesadresser tildelt vil være sammenhængende så hurtigere at få adgang til. tildelte hukommelsesadresser kan være fragmenteret så langsommere at få adgang til.
strukturer er en fast størrelse, hvilket gør dem mere forudsigelige at arbejde med. For eksempel kan de indeholde en overskrift. strukturer varierer i størrelse, så der skal være en mekanisme til at kende størrelsen på den aktuelle struktur.
forholdet mellem forskellige dataelementer ændres ikke. forholdet mellem forskellige dataelementer ændres, når programmet køres.

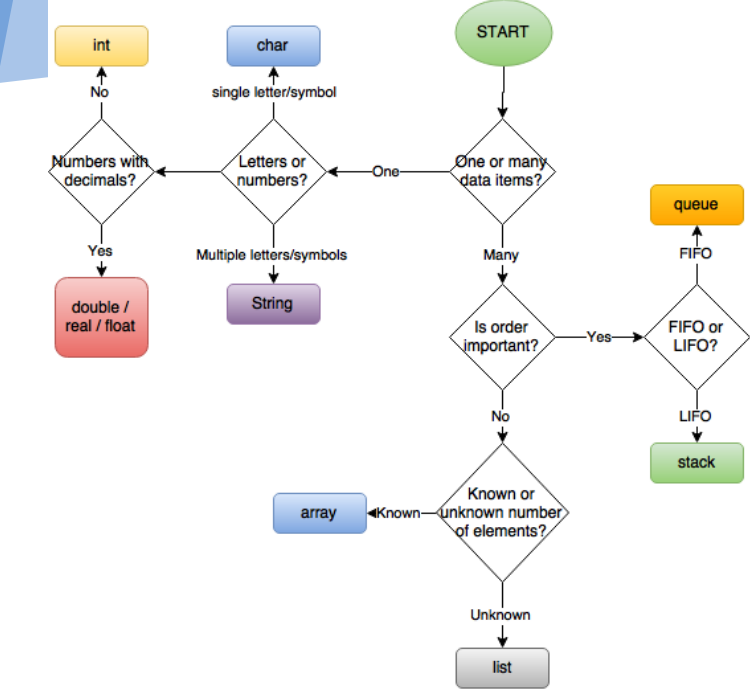
valg af hvilken datastruktur der skal bruges

denne grafik bruges med enorm taknemmelighed fra Dartford Grammar School Computer Science Department.

valg af datatype rutediagram.PNG

standarder

  • Identificer en situation, der kræver brug af rekursiv tænkning.
  • Identificer rekursiv tænkning i en specificeret problemløsning.
  • spor en rekursiv algoritme for at udtrykke en løsning på et problem.
  • beskriv egenskaberne ved et todimensionelt array.
  • Konstruer algoritmer ved hjælp af todimensionale arrays.
  • beskrive egenskaber og anvendelser af en stak.
  • Konstruer algoritmer ved hjælp af adgangsmetoderne for en stak.
  • beskrive egenskaber og anvendelser af en kø.
  • Konstruer algoritmer ved hjælp af adgangsmetoderne i en kø.
  • Forklar brugen af arrays som statiske stakke og køer.
  • beskriv funktionerne Og egenskaberne ved en dynamisk datastruktur.
  • Beskriv, hvordan sammenkædede lister fungerer logisk.
  • skitse sammenkædede lister (enkelt, dobbelt og cirkulær).
  • beskrive egenskaber og anvendelser af en samling.
  • Konstruer algoritmer ved hjælp af adgangsmetoderne i en samling.
  • diskutere behovet for delprogrammer og samlinger inden for programmerede løsninger.
  • Konstruer algoritmer ved hjælp af foruddefinerede underprogrammer, endimensionelle arrays og/eller samlinger.
  • Beskriv hvordan træer fungerer logisk (både binært og ikke-binært).
  • Definer vilkårene: forældre, venstre-barn, højre-barn, undertræ, rod og blad.
  • Angiv resultatet af inorder, postorder og preorder tree traversal.
  • skitse binære træer.
  • Definer udtrykket dynamisk datastruktur.
  • Sammenlign brugen af statiske og dynamiske datastrukturer.
  • foreslå en passende struktur til en given situation.