indtægter er det beløb, et firma bringer ind. I dette tilfælde kan indtægterne findes ved at gange prisen pr. Vi kan introducere variabler, p for pris pr. abonnement og K for mængde, hvilket giver os ligningen \tekst{indtægter}=pk.

fordi antallet af abonnenter ændres med prisen, skal vi finde et forhold mellem variablerne. Vi ved, at p=30 og P=84.000. Vi ved også, at hvis prisen stiger til $32, vil avisen miste 5.000 abonnenter, hvilket giver et andet par værdier, p=32 og K=79.000. Herfra kan vi finde en lineær ligning, der vedrører de to størrelser. Hældningen vil være

\ begin{align}m & = \ dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5.000}{2} \\ &=-2.500 \end{align}

dette fortæller os, at papiret vil miste 2.500 abonnenter for hver dollar, de hæver prisen. Vi kan derefter løse for y-skæringspunktet.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\tekst{Revenue}=p \ \ \&\tekst{Revenue}=p\left(-2.500 p+159.000 \ right) \ \&\tekst{revenue}=-2.500{p}^{2}+159.000 p \ end{align}

Vi har nu en kvadratisk funktion for indtægter som en funktion af abonnementsafgiften. For at finde den pris, der maksimerer indtægterne for avisen, kan vi finde toppunktet.

\begin{align}h&=-\dfrac{159.000}{2\left(-2.500\right)} \\ & =31.8 \ end{align}

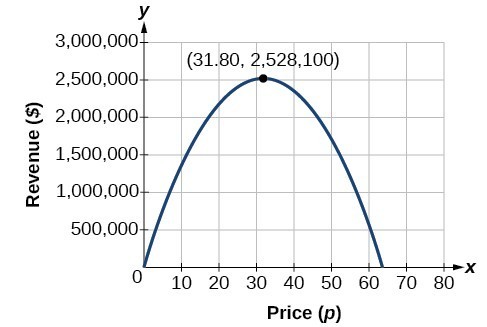
modellen fortæller os, at den maksimale omsætning vil forekomme, hvis avisen opkræver $31,80 for et abonnement. For at finde ud af, hvad den maksimale omsætning er, vurderer vi indtægtsfunktionen.

\begin{align}\tekst{maksimal omsætning}&=-2.500{\left(31.8\right)}^{2}+159.000\left(31.8\right) \\ &=\$2.528.100\hfill \end{align}

analyse af opløsningen

dette kunne også løses ved at tegne den kvadratiske. Vi kan se de maksimale indtægter på en graf over den kvadratiske funktion.