Articles

College fysik

by admin juni 24, 2021

Resume

beskriv virkningerne af en magnetisk kraft på en strømbærende leder.
Beregn den magnetiske kraft på en strømbærende leder.

fordi ladninger normalt ikke kan undslippe en leder, overføres den magnetiske kraft på ladninger, der bevæger sig i en leder, til selve lederen.

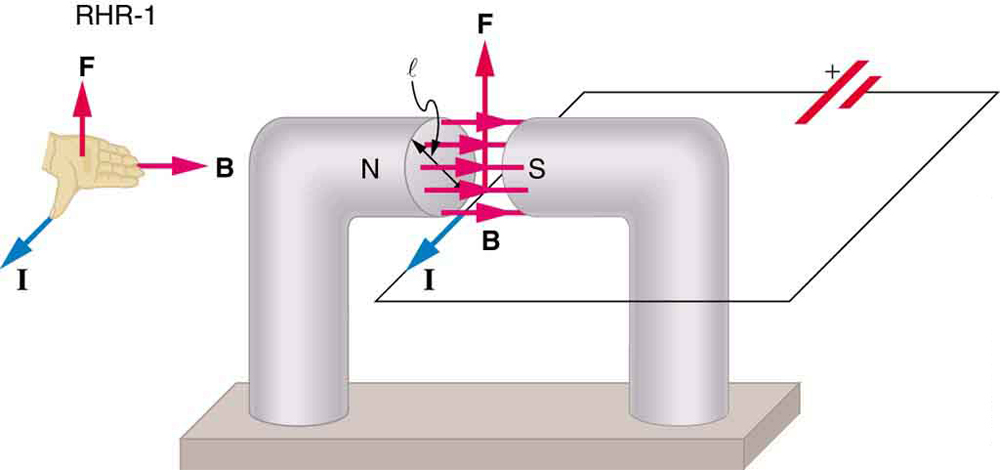
et diagram, der viser et kredsløb med strøm Jeg løber igennem det. Et afsnit af ledningen passerer mellem Nord-og Sydpolen af en magnet med en diameter l. magnetfelt B er orienteret mod højre, fra nord til Sydpolen af magneten, over ledningen. Strømmen løber ud af siden. Kraften på ledningen er rettet op. En illustration af højre håndregel 1 viser tommelfingeren, der peger ud af siden i retning af strømmen, fingrene peger lige i retning af B, og F-vektoren peger op og væk fra håndfladen. — Figur 1. Magnetfeltet udøver en kraft på en strømbærende ledning i en retning givet af højre håndregel 1 (den samme retning som på de enkelte bevægelige ladninger). Denne kraft kan let være stor nok til at bevæge ledningen, da typiske strømme består af meget stort antal bevægelige ladninger.

Vi kan udlede et udtryk for den magnetiske kraft på en strøm ved at tage en sum af de magnetiske kræfter på individuelle ladninger. (Kræfterne tilføjer, fordi de er i samme retning.) Kraften på en individuel ladning, der bevæger sig ved drivhastigheden vdvd, er givet af \boldsymbol{F = kv_db \;\tekstbf{sin} \;\theta}. Ved at tage \ boldsymbol{B} for at være ensartet over en længde af tråd \boldsymbol{l} og nul andetsteds, er den samlede magnetiske kraft på ledningen derefter \boldsymbol{F = (kv_db \;\tekstbf{sin} \;\theta)(N)}, hvor \boldsymbol{N} er antallet af ladningsbærere i sektionen af tråd af længde \boldsymbol{l}. Nu, \ boldsymbol{N=nV}, hvor \ boldsymbol{n} er antallet af ladningsbærere pr. Når man bemærker, at \boldsymbol{V=Al}, hvor \boldsymbol{A} er trådens tværsnitsareal, er kraften på ledningen \boldsymbol{F=(vv_db \;\tekstbf{sin} \;\theta)(nAl)}. Indsamling vilkår,

\boldsymbol{F=(nkav_d)lB \;\tekstbf{sin} \;\theta}.

fordi \boldsymbol{nkav_d = i} (Se kapitel 20.1 nuværende),

\boldsymbol{f = IlB \;\tekstbf{sin} \;\theta}

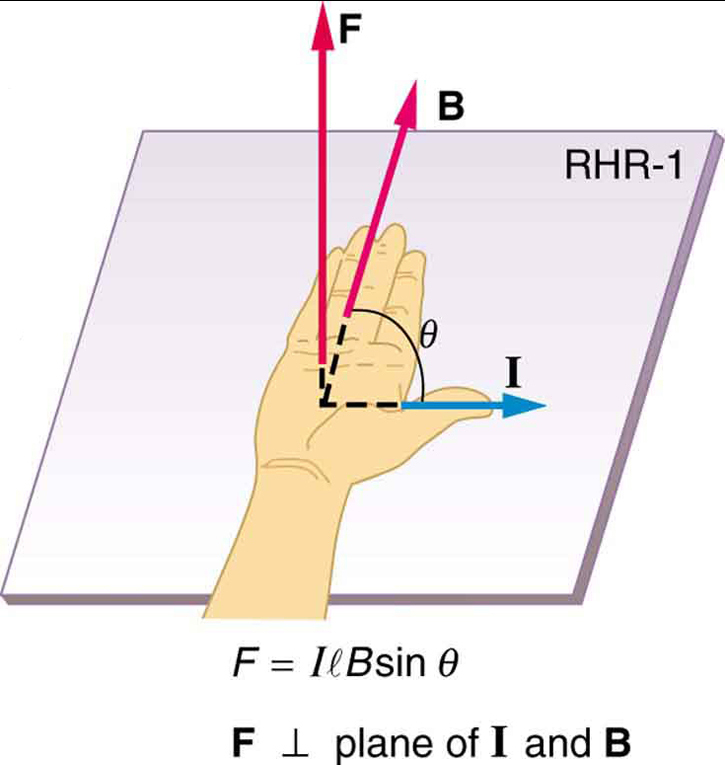
er ligningen for magnetisk kraft på en længde \boldsymbol{l} af ledning, der bærer en strøm \boldsymbol{I} i et ensartet magnetfelt \boldsymbol{B}, som vist i figur 2. Hvis vi deler begge sider af dette udtryk med \boldsymbol{l}, finder vi, at den magnetiske kraft pr.ledningslængde i et ensartet felt er \boldsymbol{\frac{F}{l} = IB \;\tekstbf{sin} \;\theta}. Retningen af denne kraft er givet af RHR-1, med tommelfingeren i retning af den nuværende \boldsymbol{i}. Derefter, med fingrene i retning af \boldsymbol{B}, peger en vinkelret på håndfladen i retning af \boldsymbol{F}, som i figur 2.

Illustration af højre håndregel 1, der viser tommelfingeren, der peger lige i retning af strøm I, fingrene peger ind på siden med magnetfelt B, og kraften rettet op, væk fra håndfladen. — figur 2. Kraften på en strømbærende ledning i et magnetfelt er F = IlB synden. Dens retning er givet af RHR-1.

beregning af magnetisk kraft på en strømbærende ledning: Et stærkt magnetfelt

Beregn kraften på ledningen vist i Figur 1, givet \boldsymbol{B = 1.50 \;\tekstbf{T}}, \boldsymbol{l = 5.00 \;\tekstbf{cm}} og \boldsymbol{I = 20.0 \;\tekstbf{a}}.

strategi

kraften kan findes med den givne information ved at bruge \boldsymbol{F = IlB \; \ tekstb{sin} \; \ theta} og bemærke, at vinklen \ boldsymbol {\theta} mellem \ boldsymbol{I} og \ boldsymbol{B} er \ boldsymbol{90 ^{\circ}}, så \ boldsymbol {\tekstbf {sin}\; \ theta = 1}.

opløsning

indtastning af de givne værdier i \ boldsymbol{F = IlB \;\tekstbf{sin} \ theta} giver

\boldsymbol{F = IlB \;\tekstbf{sin} \theta = (20.0 \;\tekstbf{a}) \; (0.0500 \;\tekstbf{m}) \; (1.50 \;\tekstbf{T}) \; (1)}.

enhederne til tesla er \boldsymbol{1 \;\tekstbf{T} = \frac{\tekstbf{N}}{\tekstbf{A} \cdot \; \tekstbf{m}}}; således

\boldsymbol{F = 1.50 \;\tekstbf{N}}.

Diskussion

dette store magnetfelt skaber en betydelig kraft på en lille ledningslængde.

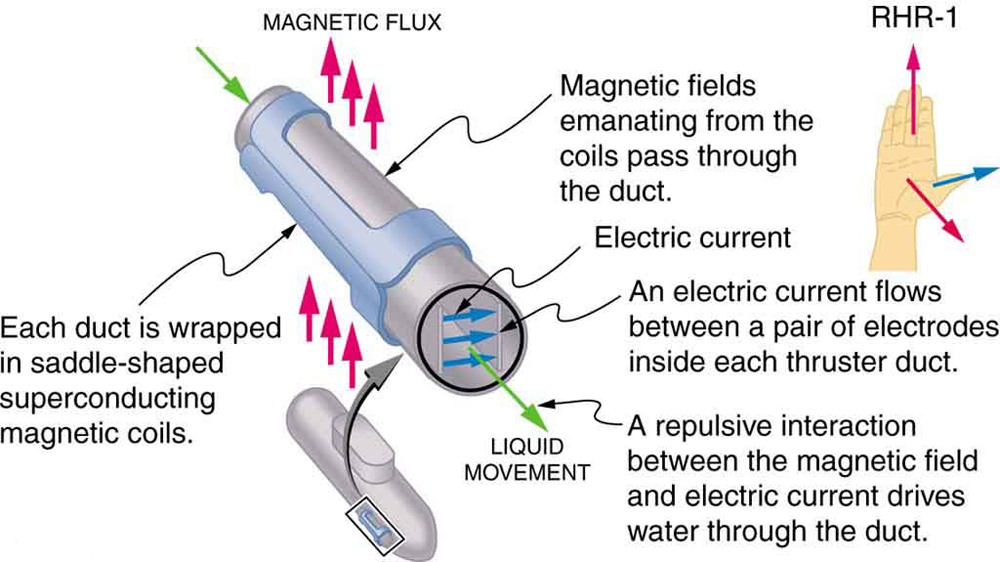
magnetisk kraft på strømbærende ledere bruges til at konvertere elektrisk energi til arbejde. (Motorer er et godt eksempel—de anvender sløjfer af tråd og overvejes i næste afsnit.) Magnetohydrodynamics (MHD) er det tekniske navn, der gives til en smart applikation, hvor magnetisk kraft pumper væsker uden at flytte mekaniske dele. (Se Figur 3.)

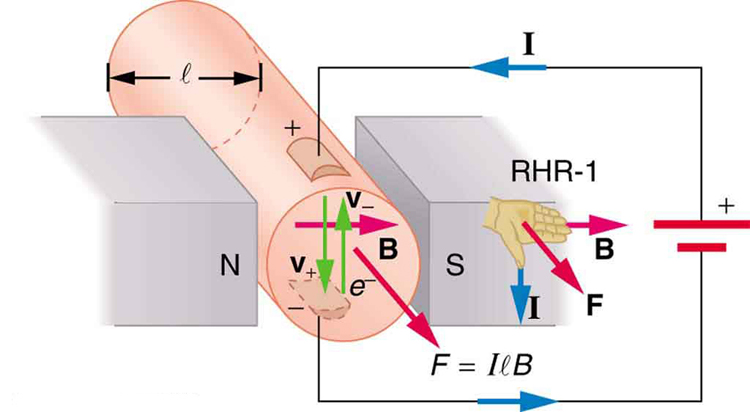
Diagram, der viser en cylinder med væske med diameter l placeret mellem en magnets Nord-og sydpoler. Nordpolen er til venstre. Sydpolen er til højre. Cylinderen er orienteret ud af siden. Magnetfeltet er orienteret mod højre, fra nord til Sydpolen og på tværs af væskecylinderen. En strømbærende ledning løber gennem væskecylinderen med strøm i orienteret nedad, vinkelret på cylinderen. Negative ladninger i væsken har en hastighedsvektor, der peger op. Positive ladninger i væsken har en hastighedsvektor, der peger nedad. Kraften på væsken er ude af siden. En illustration af højre håndregel 1 viser tommelfingeren, der peger nedad med strømmen, fingrene peger til højre med B, og kraft F orienteret ud af siden, væk fra håndfladen. — figur 3. Magnetohydrodynamik. Den magnetiske kraft på strømmen, der føres gennem denne væske, kan bruges som en ikke-mekanisk pumpe.

et stærkt magnetfelt påføres over et rør, og en strøm ledes gennem væsken vinkelret på feltet, hvilket resulterer i en kraft på væsken parallelt med røraksen som vist. Fraværet af bevægelige dele gør dette attraktivt til at flytte et varmt, kemisk aktivt stof, såsom Det flydende natrium, der anvendes i nogle atomreaktorer. Eksperimentelle kunstige hjerter tester med denne teknik til pumpning af blod, måske omgå de negative virkninger af mekaniske pumper. (Cellemembraner påvirkes imidlertid af de store felter, der er nødvendige i MHD, hvilket forsinker dets praktiske anvendelse hos mennesker.) MHD-fremdrift til atomubåde er blevet foreslået, fordi det kunne være betydeligt mere støjsvage end konventionelle propeldrev. Den afskrækkende værdi af atomubåde er baseret på deres evne til at skjule og overleve en første eller anden atomangreb. Når vi langsomt demonterer vores atomvåbenarsenaler, vil ubådsgrenen være den sidste, der bliver nedlagt på grund af denne evne (se figur 4.) Eksisterende MHD-drev er tunge og ineffektive—meget udviklingsarbejde er nødvendigt.

Diagram, der viser en forstørrelse til et magnetohydrodynamisk fremdriftssystem på en atomubåd. Væske bevæger sig gennem thrusterkanalen, som er orienteret ud af siden. Magnetfelter stammer fra spolerne og passerer gennem en kanal. Den magnetiske strømning er orienteret opad vinkelret på kanalen. Hver kanal er pakket ind i sadelformede superledende spoler. En elektrisk strøm løber til højre gennem væsken og vinkelret på væskens hastighed. Den elektriske strøm strømmer mellem et par elektroder inde i hver thruster kanal. En frastødende interaktion mellem magnetfeltet og elektrisk strøm driver vand gennem kanalen. En illustration af højre håndregel viser tommelfingeren, der peger til højre med den elektriske strøm. Fingrene peger op med magnetfeltet. Kraften på væsken er orienteret ud af siden, væk fra håndfladen. — figur 4. Et MHD-fremdrivningssystem i en atomubåd kunne producere betydeligt mindre turbulens end propeller og lade det køre mere lydløst. Udviklingen af en silent drive ubåd blev dramatiseret i bogen og filmen Jagten på Røde Oktober.

den magnetiske kraft på strømbærende ledere er givet af
\boldsymbol{f = IlB \;\tekstbf{sin} \;\theta},

hvor \boldsymbol{I} er strømmen, \boldsymbol{l} er længden af en lige leder i et ensartet magnetfelt \boldsymbol{B}, og \boldsymbol{\Theta} er vinklen mellem \boldsymbol{i} og \boldsymbol{B}. Kraften følger RHR-1 med tommelfingeren i retning af \boldsymbol{i}.

konceptuelle spørgsmål

1: Tegn en skitse af situationen i Figur 1, der viser retningen af elektroner, der bærer strømmen, og brug RHR-1 til at verificere retningen af kraften på ledningen.

2: Kontroller, at retningen af kraften i et MHD-drev, som det i figur 3, ikke afhænger af tegnet på ladningerne, der bærer strømmen over væsken.

3: Hvorfor ville et magnetohydrodynamisk drev fungere bedre i havvand end i ferskvand? Også, hvorfor ville superledende magneter være ønskelige?

4: Hvilket er mere sandsynligt at forstyrre kompasaflæsninger, vekselstrøm i køleskabet eller jævnstrøm, når du starter din bil? Forklare.

problemer& øvelser

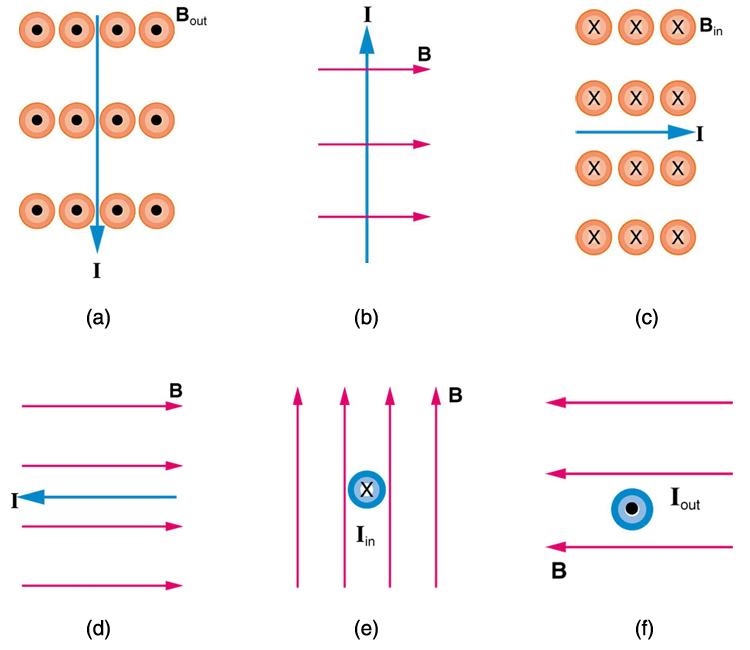
1: Hvad er retningen af den magnetiske kraft på strømmen i hvert af de seks tilfælde i figur 5?

Figur A viser magnetfeltet B ud af siden og strømmen jeg nedad. Figur b viser B mod højre og jeg opad. Figur c viser B ind på siden og jeg mod højre. Figur d viser B mod højre og jeg mod venstre. Figur e viser B opad og jeg ind på siden. Figur f viser B mod venstre og jeg ud af siden. — figur 5.

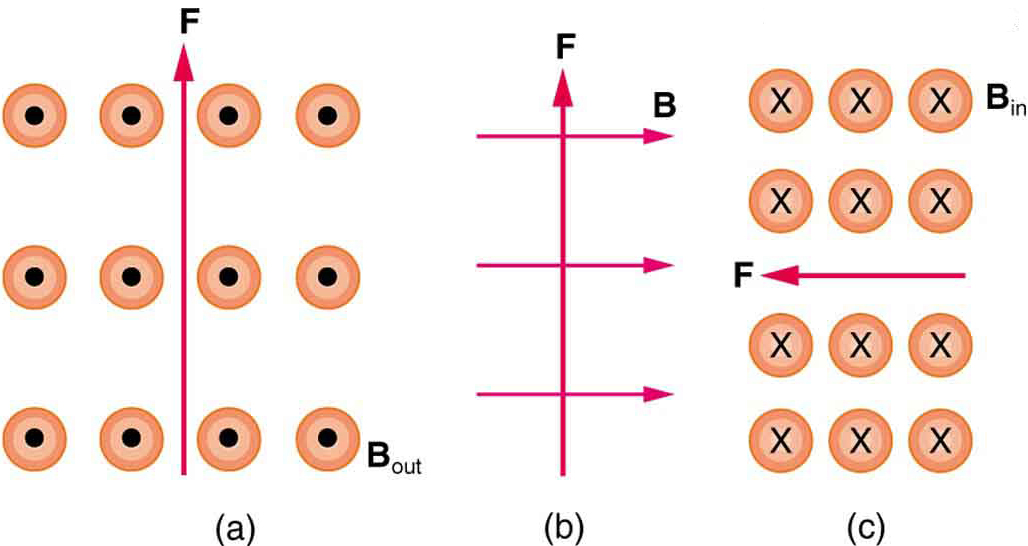
2: Hvad er retningen af en strøm, der oplever den magnetiske kraft vist i hvert af de tre tilfælde i figur 6, forudsat at strømmen løber vinkelret på \boldsymbol{B}?

Figur A viser magnetfelt B Ud af siden og tvinge F opad. Figur b viser B mod højre og F opad. Figur c viser B ind på siden og F mod venstre. — figur 6

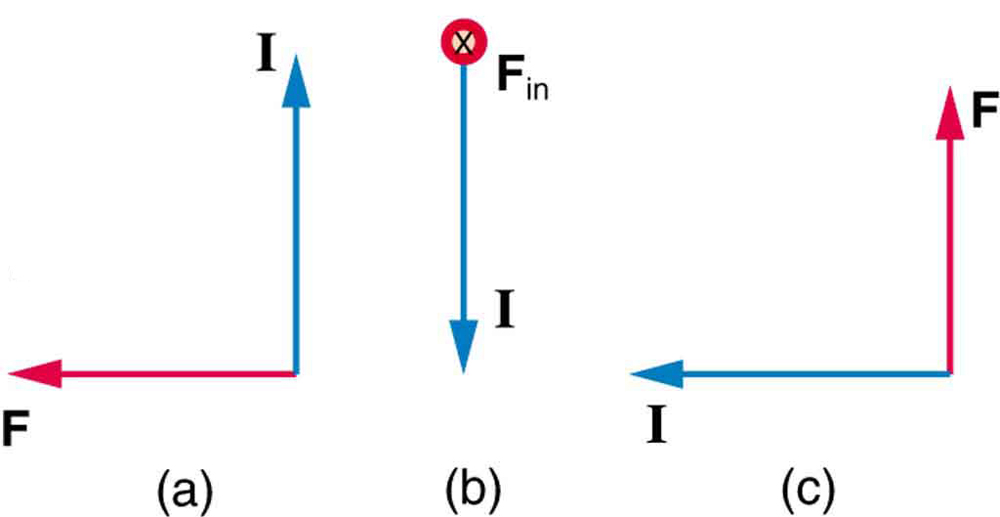
3: Hvad er retningen af magnetfeltet, der producerer den magnetiske kraft, der vises på strømmen i hvert af de tre tilfælde i Figur 7, forudsat at \boldsymbol{B} er vinkelret på \boldsymbol{i}?

Figur A viser den aktuelle i-vektor, der peger opad, og kraften F-vektor peger til venstre. Figur b viser den aktuelle vektor, der peger nedad, og F rettet ind på siden. Figur c viser den aktuelle peger til venstre og kraft peger op. — Figur 7.

4: (A) Hvad er kraften pr. meter på en lynbolt ved ækvator, der bærer 20.000 en vinkelret på jordens \boldsymbol{3.00 \gange 10^{-5} – \tekstbf{t}} felt? (b) Hvad er kraftens retning, hvis strømmen er lige op og Jordens feltretning er ret nord, parallelt med jorden?

5: (a) en JÆVNSTRØMSLEDNING til et letbanesystem bærer 1000 A i en vinkel på \boldsymbol{30,0 ^{\circ}} til Jordens \boldsymbol{5,00 \gange 10^{-5}-\tekstbf{t}} felt. Hvad er kraften på en 100 m sektion af denne linje? B) drøfte eventuelle praktiske forhold, som dette giver anledning til.

6: hvilken kraft udøves på vandet i et MHD-drev ved hjælp af et rør med en diameter på 25,0 cm, Hvis 100-A strøm føres over røret, der er vinkelret på et 2,00-t magnetfelt? (Den relativt lille størrelse af denne kraft indikerer behovet for meget store strømme og magnetfelter til at lave praktiske MHD-drev.)

7: en ledning, der bærer en 30,0-a strøm, passerer mellem polerne på en stærk magnet, der er vinkelret på dens felt og oplever en 2,16-n kraft på 4,00 cm ledning i marken. Hvad er den gennemsnitlige feltstyrke?

8: (A) en 0,750 m lang sektion af kabelbærende strøm til en bilstartmotor gør en vinkel på \boldsymbol{60^{\circ}} med jordens \boldsymbol{5,50 \gange 10^{-5} \;\tekstbf{t}} felt. Hvad er strømmen, når ledningen oplever en kraft af \boldsymbol{7.00 \gange 10^{-3} \;\tekstbf{n}}? (b) hvis du kører ledningen mellem polerne på en stærk hesteskomagnet og udsætter 5,00 cm af den for et 1,75-t felt, hvilken kraft udøves på dette trådsegment?

9: (A) Hvad er vinklen mellem en ledning, der bærer en 8,00-a strøm og 1,20-t-feltet, den er i, hvis 50,0 cm af ledningen oplever en magnetisk kraft på 2,40 n? (b) Hvad er kraften på ledningen, hvis den drejes for at lave en vinkel på \boldsymbol{90^{\circ}} med feltet?

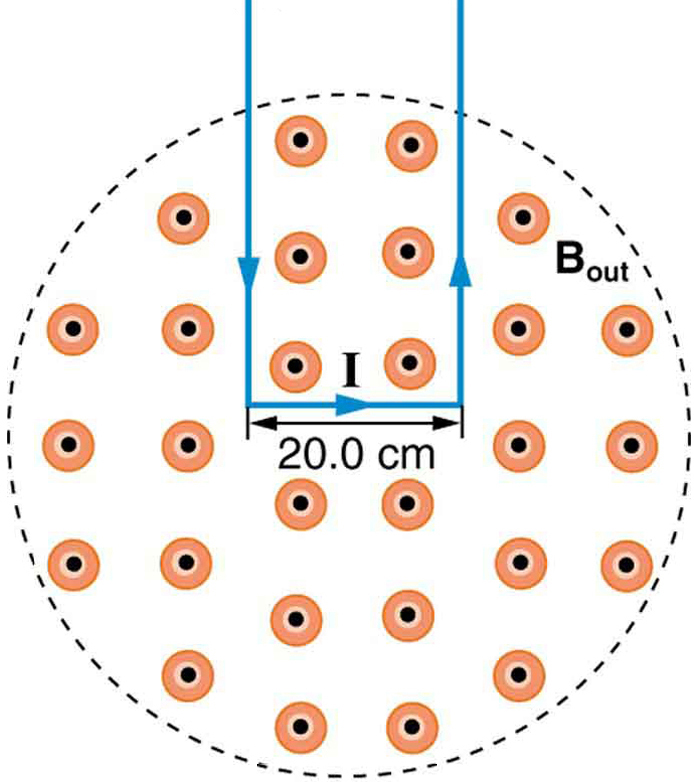
10: kraften på den rektangulære trådsløjfe i magnetfeltet i figur 8 kan bruges til at måle feltstyrke. Feltet er ensartet, og sløjfens plan er vinkelret på feltet. (a) Hvad er retningen af den magnetiske kraft på sløjfen? Begrund påstanden om, at kræfterne på siderne af løkken er lige og modsatte, uafhængigt af hvor meget af løkken der er i marken og ikke påvirker nettokraften på løkken. (B) hvis der anvendes en strøm på 5,00 a, Hvad er kraften pr. tesla på den 20,0 cm brede sløjfe?

Diagram, der viser en rektangulær trådsløjfe, hvis ene ende er inden for et magnetfelt, der er til stede inden for et cirkulært område. Feltet B er orienteret ud af siden. Strømmen jeg løber i sidens plan, ned i venstre side af kredsløbet, mod højre i bunden af kredsløbet og opad på højre side af kredsløbet. Længden af trådsegmentet, der løber fra venstre mod højre i bunden af kredsløbet, er tyve centimeter lang. — figur 8.

løsninger

problemer & øvelser

1: (A) vest (venstre)

(b) til side

(d) ingen kraft

(E) øst (højre)

(f) syd (ned)

3: (a) ind på side

(b) vest (venstre)

5: (a) 2.50 n

(b) dette er omkring et halvt pund 100 m ledning, hvilket er meget mindre end selve trådens vægt. Derfor giver det ingen særlige bekymringer.

7: 1, 80 T

9: (a) \boldsymbol{30^{\circ}}

(b) 4.80 N

Micro Blogs